Автоматическая классификация текстовых документов с использованием нейросетевых алгоритмов и семантического анализа

Андреев А.М., Березкин Д.В., Морозов В.В., Симаков К.В.

Введение

Классификация текстовых документов для электронных библиотек рассматривается как один из возможных вариантов решения проблемы использования информационных ресурсов. Коротко она характеризуется следующим образом. К настоящему моменту различными хранилищами знаний (в том числе и библиотеками) накоплены огромные информационные массивы. Проблема заключается в сложности ориентирования в этих массивах, адекватной их размерам. Отсутствие возможности получить наиболее актуальную и полную информацию по конкретной теме делает бесполезной большую часть накопленных ресурсов. Поскольку исследование конкретной задачи требует все больших трудозатрат на непосредственный поиск и анализ информации по теме, многие решения принимаются на основе неполного представления о проблеме.

Использование рубрикаторов-классификаторов позволяет сократить трудозатраты на поиск нужной информации, представленной электронными текстами. Применение семантического  анализа, позволяет повысить релевантность такого поиска, в то время как использование искусственных нейронных сетей упрощает процедуру построения классификатора.

1. Формализация задачи

Классификацию текстов на естественном языке (ТЕЯ) называют рубрицированием, поэтому в дальнейшем изложении эти термины принимаются идентичными. Рубрикаторы подразделяются на три основных класса: плоские, иерархические и сетевые. Плоские рубрикаторы состоят из двух уровней, на первом уровне размещается корневая, а на втором – дочерние к корневой рубрики. Как показано в [12], иерархические и сетевые рубрикаторы могут быть представлены в виде композиции нескольких плоских рубрикаторов, поэтому в статье рассматриваются только плоские рубрикаторы.

1.1. Задача классификации

Задача классификации определяется следующим образом. Имеется множеств объектов T , не обязательно конечное, а так же множество C={ci} i=1..Nc , состоящее из Nc классов объектов. Каждый класс ci представлен некоторым описанием Fi , имеющим некоторую внутреннюю структуру. Процедура классификации f объектов t T заключается в выполнении преобразований над ними, после которых либо делается вывод о соответствии t одной из структур Fi , что означает отнесение t к классу ci , либо вывод о невозможности классификации t. Применительно к ТЕЯ, элементами множества T являются электронные версии текстовых документов. Общая модель плоского текстового рубрикатора (ПТР) может быть представлена трех основной алгебраической системой следующего вида (1).

где T – множество текстов, подлежащих рубрицированию, C - множество классов-рубрик, F – множество описаний, Rc – отношение на C x F, f – операция рубрицирования вида T C. Отношение Rc имеет свойство: , то есть классу соответствует единственное описание. Обратное требование необязательно. Отображение f не имеет никаких ограничений, так что возможны ситуации, когда, то есть некоторый текст может быть отнесен к нескольким классам одновременно. Кроме сформулированной задачи классификации определяется задача обучения рубрикатора, под которой подразумевается частичное или полное формирование C, F, Rc и f на основе некоторых априорных данных.

1.2. Основные виды классификаторов

Согласно выражению (1) ПТР могут быть разде­лены в зависимости от способа представления опи­саний классов (внутренняя структура элементов множества F), а так же от организации процедуры классификации f. В настоящее время практическое применение получили следующие группы.

1. Статистические классификаторы, на основе вероятностных методов. Наиболее известным в данной группе является семейство Байесовых. Общей чертой для таких ПТР является процедура f, в основе которой лежит формула Байеса для условной вероятности. Анализируемый текст t представляется в виде последовательности терминов {wk}. Каждая рубрика ci характеризуется безусловной вероятно­стью ее выбора P(ci) в процессе классификации некоторого документа (совокупность таких событий для всех рубрик образуют систему гипотез, так что ), а так же условной вероятностью P(w|ci) встретить термин w в документе t при условии выбора рубрики ci. Эти величины образуют элементы Fi множества F описаний рубрик и используются при расчете вероятностей P(t|ci) того, что текст будет классифицирован при условии выбора рубрики ci. При расчете P(t|ci) учитывается представление t в виде последовательности терминов wk. Подстановка этих величин в формулу Байеса дает вероятность того, что будет выбрана рубрика ci, при условии, что документ t пройдет успешную классификацию. Процедура f сводится к подсчету P(ci|t) для всех рубрик ci и выбора той, для которой эта величина максимальна. Обучение рубрикатора сводится к составлению словаря {wn} и определению для каждой рубрики величин P(ci) и P(w|ci), где w{wn}.

2. Классификаторы, использующие методы на основе искусственных нейронных сетей. Данный вид классификаторов хорошо зарекомендовал себя  в задачах распознавания изображений, в данной работе исследованы возможности их использования в обработке ТЕЯ. Описания классов F, как правило, представляют собой многомерные вектора действительных чисел, заложенные в синаптических весах искусственных нейронов, а процедура классификации f характеризуется способом преобразования анализируемого текста t к аналогичному вектору, видом функции активации нейронов, а так же топологией сети. Процесс обучение классификатора в данном случае совпадает с процедурой обучения сети и зависит от выбранной топологии. В данной работе рассматриваются ПТР, построенные на основе популярных сетей ART и SOM.

3. Классификаторы, основанные на функциях подобия. Характерной чертой данного метода является универсальность описаний F, которые с одной стороны используются для представления содержания рубрик, а с другой стороны – содержания анализируемых текстов. Процедура классификации f использует меру подобия вида E: F x F[0;1], позволяющую количественно оценивать тематическую близость описаний Ft F и Fi F , где описание Ft представляет содержание анализируемого текста, а Fi – содержание некоторой рубрики. Действия процедуры классификации f сводятся к преобразованию анализируемого текста t в представление Ft F, оценке подобия описания Ft с описаниями рубрик Fi (вычисление E(Ft,Fi)), и заключение по результатам сопоставления о принадлежности текста одой или нескольким рубрикам. Последнее заключение выполняется либо на основе сравнения с пороговой величиной Emin, так что текст относится ко всем рубрикам ci, для которых E(Ft,Fi)>Emin, либо из всех E(Ft,Fi) выбирается максимальная величина, которая и указывает на результирующую рубрику. Наиболее характерными для таких классификаторов является использование лексических векторов модели терм-документ (см. в [3]) в описаниях F, которые так же применяются и в нейронных классификаторах. В качестве меры подобия обычно берется косинус угла между векторами, вычисляемый через скалярное произведение согласно (2).

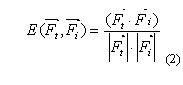
В более сложных моделях текста, использующих синтаксическое и семантическое представление, мера подобия может быть значительно сложнее. В данной работе затрагиваются оба способа описания, учитывающие как синтаксическую, так и семантическую составляющую.

1.3. Полнота и точность классификации

Существует несколько характеристик оценки качества работы текстового классификатора, их описание приведено в [12]. Наибольшее распространение получили точность (V) и полнота (U), применяемые так же при оценке качества естественно-языкового поиска [3] , например, в поисковых машинах сети Интернет. Для количественной оценки полноты и точности рубрикатора используются следующие измерения: a – число правильно рубрицированных документов, b – число неправильно рубрицированных документов, c – число неправильно отвергнутых документов. Под правильной и неправильной рубрикацией понимается случай, когда классификатор приписывает анализируемый документ некоторой рубрике, что расценивается некоторым экспертом соответственно, как верное и неверное решение. Под неправильным отвержением документа понимается случай, когда классификатор не приписывает документ рубрике, что, по мнению эксперта, неверно. На рис. 1 дана иллюстрация этих случаев.

Рис.1. Соотношение оценки эксперта и рубрикатора.

С учетом этого, оценка V и U имеет вид (3).

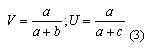
Согласно (3), точность оценивает долю правильно классифицированных документов во всех документах отнесенных к некоторой рубрике. Полнота оценивает долю правильно классифицированных документов во всех документах, которые НУЖНО было отнести к некоторой рубрике.

2. Нейросетевые классификаторы

Нейронные сети могут применяться при решении многих задач обработки информации, в частности в задачах распознавания образов. Как известно, искусственный (математический) нейрон выполняет следующие преобразования входного вектора X={xi}: , где wi – весовой вектор нейрона (веса синаптических связей), S – результат взвешенного суммирования, I – нелинейная функция активации нейрона. В терминах классификатора (1) X – соответствует внутренним описаниям {Fi}, а функции S и I – компоненты процедуры классификации f. Функциональность нейрона проста, поэтому для решения конкретных задач нейроны объединяются в сети. Обучение классификатора, при условии, что выбрана топология сети и выбрана функция активации I, сводится к подбору весовых коэффициентов каждого нейрона. В данной работе рассматривается применение двух топологий: сети ART и сети Кохонена.

2.1. Способы представления текста

Нейронные сети приспособлены обрабатывать только информацию, представленную числовыми векторами, поэтому для их применения в обработке ТЕЯ, тексты необходимо представлять в векторном виде. В данной работе использовались два способа представления: полиграммная модель и модель терм – документ.В модели терм – документ [3] текст описывается лексическим вектором {} i=1..Nw, где – важность (информативный вес) термина wi в документе,  Nw – полное количество терминов в документальной базе (словаре). Вес термина, отсутствующего в документе, принимается равным 0. Для удобства веса нормируются, так что [0,1]. В данной работе использовались дискретные значения, так что присутствующий термин в тексте имеет вес 1, а отсутствующий – вес 0. Достоинствами данной модели являются:

●     возможный учет морфологии, когда все формы одного слова соответствуют одному термину;

●     возможный учет синонимии, так что слова - синонимы, объявляются одним термином словаря;

●     возможность учета устойчивых словосочетаний, так что в качестве термина может выступать не отдельное слово, а несколько связанных слов, образующих единое понятие.

В качестве недостатков выделим следующее:

●     при отсутствии простейшей дополнительной обработки, такой как морфологический анализ, существенно снижается качество классификатора, поскольку разные формы одного слова считаются разными терминами, вместе с тем морфологический анализ – весьма нетривиальная задача, требующая для ее решения привлечения лингвистов;

●     размерность векторов {} зависит от общего количества терминов в обучающей выборке текстов, что в реальных задачах приводит к необходимости разрабатывать альтернативные структуры данных, отличные от векторов;

●     словарь терминов может не охватывать всех документов, подлежащих классификации, так что анализируемые документы могут содержать значимые термины, не вошедшие в обучающую выборку, что отрицательно сказывается на адекватности модели.

В полиграммной модели со степенью n и основанием M текст представляется вектором {fi}, i=1..Mn, где fi – частота встречаемости i-ой n-граммы в тексте. n-грамма является последовательностью подряд идущих n – символов вида a1…an-1an, причем символы ai принадлежат алфавиту, размер которого совпадает с M. Непосредственно номер n-граммы  определяется как , где  r(ai ) [1,M] – порядковый номер символа ai в алфавите. Предполагается, что частота появления n-граммы в тексте несет важную информацию о свойствах документа. В данной работе рассмотрена модель со степенью n=3 (триграммная модель) и основанием M=33, при этом применяется русский алфавит с естественной нумерацией символов r("А") = 1, r("Б") = 2, ..., r("Я") = 32. Все остальные символы считаются пробелами с нулевыми номерами. Несколько подряд идущих пробелов считаются одним.  С учетом этого размерность вектора  для произвольного текста жестко фиксирована и составляет 333 = 35937 элемента. Достоинствами полиграммной модели являются:

●     отсутствие необходимости дополнительной лингвистической обработки;

●     фиксированная размерность векторов и простота получения векторного описания текста;

К недостаткам отнесем следующее:

●     отражение векторами {fi} содержания текста не всегда адекватно (такой моделью плохо отражается содержание небольших текстов; модель больше подходит для определения языка текста, чем для классификации по тематике),

●     в соответствии с предыдущим пунктом возникает необходимость более тщательного подбора обучающей выборки текстов.

2.2. Классификатор Гроссберга (ART)

Сеть ART [11] состоит из двух слоев нейронов (рис 2). Первый (входной) слой – сравнивающий, второй слой – распознающий.  В общем случае между слоями существуют прямые связи с весами wij от i – ого нейрона входного слоя к j – ому нейрону распознающего слоя, обратные связи с весами vij – от i-ого нейрона распознающего слоя к j – ому нейрону входного слоя. Так же существуют латеральные тормозящие связи между нейронами распознающего слоя (пунктир на рис. 2). Каждый нейрон распознающего слоя отвечает за один класс объектов. Веса wij используются на первом шаге классификации для выявления наиболее подходящего нейрона – класса, веса обратных связей vij хранят типичные образы (прототипы) соответствующих классов и используются для непосредственного сопоставления с входным вектором.

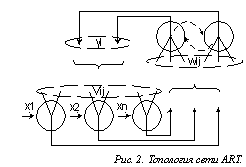
Рис. 2. Топология сети ART.

Согласно назначению приведенных компонентов такой сети роцедура классификации представляет собой следующую последовательность операций:

1. вектор X подается на вход сети, для каждого нейрона распознающего слоя определяется взвешенная сумма его входов.

2. за счет латеральных тормозящих связей распознающего слоя на его выходах устанавливается единственный сигнал с наибольшим значением, остальные выходы становятся близкими к 0.

3. 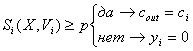входной вектор сравнивается с прототипом класса Vi, соответствующего i-ому нейрону, победившему на предыдущем шаге. Если результат сравнения превышает порог p, делается вывод о том, что входной вектор принадлежит классу ci, в противном случае выход данного нейрона обнуляется (принудительная блокировка) и повторяется процедура на шаге 2, в которой за счет обнуления самого активного нейрона  происходит выбор нового.

4. Шаги 2-3 повторяются до тех пор, пока не будет получен класс cout, либо пока не будут принудительно заблокированы все нейроны распознающего слоя.

Поскольку многие компоненты сети на рис. 2 необходимы для аппаратной реализации сети, в программе классификатора многие из них могут быть опущены, а именно: убираются связи латерального торможения, вместо двух матриц Wij и Vij используется одна – Wij, которая отвечает и за выбор предпочтительного нейрона-класса, и за хранение прототипов классов. В этом случае вычисление функции сопоставления S совмещает в себе шаги 2 и 3 и рассчитывается непосредственно для X и весовых векторов Wi, побеждает тот нейронi , для которого max (Si). Для обучения сети, кроме Si используется еще одна мера Si'  близости векторов 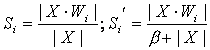(5)

где , , , b - положительная константа. Алгоритм обучения [1] состоит из следующих шагов.

1. На входы подать обучающий вектор X<. Активизировать все нейроны выходного слоя.

2. Найти активный нейрон с прототипом Wi, наиболее близким к X, используя меру близости Si.

3. Если для найденного нейрона 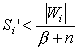или еще нет ни одного класса, то создать новый класс Wi и идти на шаг 1.

4. Если для найденного нейрона , то деактивировать найденный нейрон. Если все нейроны неактивны, то создать новый класс Wi = X, идти на шаг 1. Иначе идти на шаг 2 и попробовать другой еще активный нейрон.

5. Если для найденного нейрона Si' и Si превышают пороги, указанные на шаге 4 и 5, то модифицировать его веса , передвинув ближе к входному вектору.

На количество образующихся классов оказывают влияние константы и .С ростом и уменьшением их количество увеличивается. Коэффициент обучения 0 < < 1 определяет скорость обучения. В начале обучения его значения должно быть большим и монотонно уменьшаться со временем.

Классификация документов сводится к предъявлению обученной нейронной сети вектора авизируемого текста X и поиска из всех нейронов распознающего слоя того, для которого Siнаибольшая. При использовании в качестве входных векторов представление текста в виде лексических векторов модели терм-документ,входной слой содержит столько нейронов, сколько терминов в словаре обучающей выборки документов (Nw),  весовые вектора Wi нейронов распознающего слоя содержат значимость wji j -ого термина для i-ого класса. Моделирование проводилось для базы данных, состоящих из документов двух типов: сводки УВД и банковские документы (271 документ, 40315 терминов). Использовались следующие значения констант: = 0, = 0.01 = 0.7. В процессе эксперимента варьирование начальных значений  и  приводило к образованию от 2 до 22 двух кластеров. В лучшем случае классификация произвела абсолютно правильное разбиение документов на две группы: один класс соответствует сводкам УВД, другой – банковским документам.

При использовании триграммной модели представления текста число входных нейронов соответствует M3, при этом весовые вектора Wi определяют значимость wji j-ой триграммы для i-ого класса. При моделировании использовались следующие значения констант: принимала значения от 0 до 1000,  = 0.01, линейно убывала от 0.75  до 0.1. Подача на вход сети 16 документов (8 сводок УВД и 8 банковских документов) в случайной последовательности при различных значениях на первом этапе обучения приводила к образованию от 1 до 4 классов.

Основным выводом по результатам моделирования является зависимости величин полноты и точности классификации (3) от пороговых параметров и , так что снижение и увеличение снижает избирательность сети, что приводит к снижению точности и повышению полноты классификации

2.3. Сеть Кохонена (SOM)

Назначение сети Кохонена [5] – разделение векторов входных сигналов на группы, поэтому возможность представления текстов в виде векторов действительных чисел позволят применять данную сеть для их классификации. Как показано на рис. 3 сеть состоит из одного слоя, имеющего форму прямоугольной решетки для 4-х связных нейронов и форму соты для 6-ти связных.

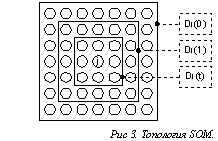
Рис 3. Топология SOM.

Анализируемые вектора Xподаются на входы всех нейронов. По результатам обучения геометрически близкие нейроны оказываются чувствительными к похожим входным сигналам, что может быть использовано в задаче классификации следующим образом. Для каждого класса определяется центральный нейрон и доверительная область вокруг него. Критерием границы доверительной области является расстояние между векторами соседних нейронов и расстояние до центрального нейрона области. При подаче на вход обученной сети вектора текста активизируются некоторые нейроны (возможно из разных областей), текст относится к тому классу, в доверительной области которого активизировалось наибольшее число нейронов и как можно ближе к ее центру.Алгоритм обучения сети заключается в следующем. Все вектора должны лежать на гиперсфере единичного радиуса. Задается мера соседства нейронов, позволяющая определять зоны топологического соседства в различные моменты времени. На рис. 3 показано изменение этой величины Dj(t) для некоторого j – ого нейрона. Кроме того, задается размер решетки и размерность входного вектора, а так же определяется мера подобия векторов S (наиболее подходящей является косинус угла, вычисляемый по формуле вида (2)). Далее выполняются следующие шаги для каждого вектора обучающей выборки.

1. Начальная инициализация плоскости может быть произведена, например произвольным распределением весовых векторов на гиперсфере единичного радиуса.

2. Сети предъявляется входной вектор текста Xи вычисляется мера подобия S(X,Wj) для каждого j – ого нейрона сети. Нейрон, для которого Sj максимальна, считается текущим центром и для него определяется зона соседства Dj(t)

3. Для всех нейронов, попадающих в зону Dj(t) (см. рис. 3) производится коррекция весов по правилу , где - шаг обучения, уменьшающийся с течением времени. Величина Dj(t) уменьшается со временем, так что изначально она охватывает всю сеть, а в конце обучения зона сужается до одного-двух нейронов, когда также достаточно мало. По аналогии с классификатором Гроссберга возможно использование как представление терм-документ, так и триграммное представление. Оба способа дали  удовлетворительные результаты в эксперименте с двумя обучающими выборками (те же что и в классификаторе Гроссберга). Как показали эксперименты, на обучение сети оказывает влияние:

1. Количество нейронов и их размещение. Количество нейронов  следует выбирать не меньше количества групп, которые требуется получить. Расположение нейронов на двумерной плоскости зависит от решаемой задачи. Как правило, выбирается либо квадратная матрица нейронов, либо прямоугольная с отношением сторон, близким к единице.

2. Начальное состояние. В данном случае применена инициализация случайными значениями. Это не всегда приводит к желаемым результатам. Один из возможных вариантов улучшения этого – вычисление характеристических векторов репрезентативной выборки текстов, определяющих границу двумерной плоскости проекции. После этого, весовые вектора нейронов равномерно распределяются в полученном диапазоне.

3. Значение коэффициента обучения. Вне зависимости от начального распределения весовых векторов нейронов при значении коэффициента скорости обучения в районе 0.5-1 образуется множество отдельных классов, хотя в целом тенденция нейронов объединяться в однотипную группу сохраняется. В данном случае можно говорить о повышенной чувствительности сети к различным входным воздействиям. При уменьшении этого коэффициента чувствительность сети падает. Так что такие показатели как полнота и точность классификации (3) определяются величиной и скоростью ее уменьшения в процессе обучения, чем быстрее убывает , тем больше точность и меньше полнота классификации.

4. Характер изменения топологической зоны соседства Dj(t). Определяет область нейронов, которые подлежат обучению. Чем быстрее будет сокращаться эта область, тем больше классов будет образовано, тем больше точность и меньше полнота.

5. Тип подаваемых на вход данных. Для лексических векторов фактически проводится обработка по имеющимся в документе термам, что дает достаточно хорошие результаты. В этом случае можно выделять документы по специфике словарного набора. Однако без применения морфологического анализа, данный метод не применим, так как резко увеличивается вычислительная сложность. Для триграммного представления текстов результаты классификации хуже, что связано с низкой адекватностью модели.

6. Последовательность подачи на вход векторов документов из разных групп.Поскольку со временем изменяется коэффициент скорости обучения , результаты подачи на вход различных векторов текстов оказываются различными. При большом начальном значении , происходит интенсивная модификация всех нейронов вокруг победителя. При этом со временем уменьшается и, если успеет уменьшиться значительно по сравнению с начальным значением до момента поступления на вход документов из следующей группы, получится довольно распределенная область, в которой встречаются документы из первой группы и сконцентрированные документы из второй группы. При случайной подаче документов из разных групп, области близости образуются равномерно. Однако возможно склеивание документов из разных групп. Причина в том, что вектор второго документа может оказаться где-нибудь поблизости от первого. В данном случае после приближения первым документов весовых векторов соседних от него нейронов, второй документ может скорректировать нейроны под себя.

3. Семантический анализ

Применение семантического анализа обусловлено стремлением улучшить качество классификации. Авторы убеждены, что, оперируя с формальным смыслом ТЕЯ, можно добиться большей полноты и точности  классификации, за счет повышения адекватности описаний F из (1). Выполнение семантического анализа осуществляет Система Понимания Текстов (СПТ). Рассмотрим принципы построения СПТ и методы, закладываемые в основу ее работы.

3.1.Определение семантического анализа

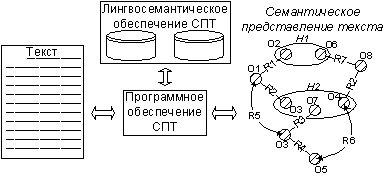
Термины семантический анализ и машинное понимание текста принимаются эквивалентными. За основу в данной работе взяты текстологические методы извлечения знаний, применяемые в инженерии знаний при разработке и ручном наполнении баз знаний экспертных систем [2,13] . При таком подходе процедуры «понимания» и «извлечения знаний» являются идентичными, а результат их выполнения формализуется в виде некоторой семантической структуры. По аналогии машинное понимание рассматривается в виде процесса  формирования семантического образа для анализируемого ТЕЯ, выполняемого СПТ (рис. 4).

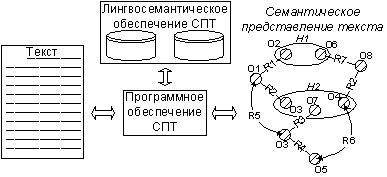
Рис.4. Функционирование СПТ.

В СПТ выделено лингвосемантическое и программное обеспечение. Первое используется для описания модели предметной области и представлено лингвистическим и семантическим словарями [6] , в терминах которых СПТ формирует образ текста [7] . Программное обеспечение реализует методы анализа, о которых пойдет речь далее. Работу СПТ можно разделить на два этапа: лингвистическая обработка и семантическая интерпретация, выполняемые соответственно лингвистическим и семантическим модулями СПТ.

Лингвистический модуль (рис. 5) объединяет этапы непосредственной ЕЯ обработки. На этих этапах происходит первичная формализация предложений входного текста. Каждый этап использует словари лингвистического обеспечения. На этапе графематического анализа выделяются текстовые единицы, такие как слова, предложения и абзацы.

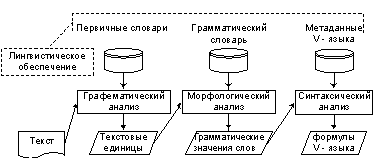
Рис.5. Схема лингвистического модуля СПТ.

Кроме того, на этом этапе выполняется исключения незначимых слов и более сложных конструкций, таких как вводные предложения. На этапе морфологического анализа определяются грамматические значения слов, такие как часть речи, род, число и т.д. На этапе синтаксического анализа определяется синтаксическая структура предложения, описываемая формулой V – языка, о котором будет сказано далее. Работа семантического модуля приведена на рис. 6.

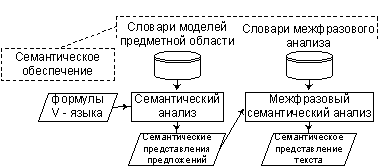
Рис.6. Схема семантического модуля СПТ.

Семантический модуль выполняет смысловую обработку текста, входные данные представлены V – формулами, полученными лингвистическим модулем. Данный вид обработки называется интерпретацией, поскольку согласно заложенной в словарях семантического обеспечения моделью предметной области выполняется определение формального смысла отдельных формул V – языка. Эта процедура выполняется на этапе семантического анализа. На этапе межфразового семантического анализа производится объединение семантических представлений отдельных предложений в единую семантическую сеть, описывающую смысл всего текста.

3.2. Формальный V - язык

В процессе семантического анализа на некоторых промежуточных стадиях получаются и используются формулы V – языка. Его основное назначение – описание морфологического и синтаксического строя предложения, описываемого V – формулой. Следует отметить, что так или иначе в лингвистических процессорах (ЛП), являющихся частным случаем СПТ, применяются те или иные способы описания результатов морфологического и синтаксического анализа. Как правило, эти результаты описываются разными конструкциями, обусловленными в первую очередь удобствами того языка программирования, на котором выполнена разработка ЛП. Авторами не были обнаружены удовлетворительные для поставленных задач средства выполнения такого описания, в результате чего и был разработан типизированный формальный V – язык, по аналогии с категориальной грамматикой, описанной в  [9]

Кроме основного назначения, благодаря вводимым в V – формулах переменным, язык позволяет описывать шаблоны синтаксических конструкций различной степени определенности и детализации. Эти возможности используются модулями СПТ для представления результатов работы морфологического и синтаксического анализатора и описания модели предметной области. Гибкость языка, так же делает возможным его независимое применение в системах, связанных с синтезом ЕЯ текстов и машинным переводом.

Ключевым звеном V – языка являются типы, приписываемые всем его объектам, синтаксис их записи следующий:

1.<тип>::=<примитив кат. 0>(<примитив кат. n1,…, примитив кат. nm; ni, nj [n1, nm]: i j ninj>

2. <примитив кат. j>::=<тип. константа. j-ой кат.>|<тип. переменная j-ой кат.>

3. <тип. константа j-ой кат. >::=<символ j-ой кат.><ID>

4. <тип. переменная j-ой кат>::=<символ j-ой кат.>x<ID>

5. <символ j-ой кат.>::=<[a..z]\’x’>

6.<ID>::=<целое число>

Каждой категории примитивов ставится в соответствие грамматическая категория естественного языка: часть речи, род, число и т.д. Каждой константе некоторой категории ставится в соответствие значение соответствующей грамматической категории: единственное/множественное число, мужской/женский/средний род и т.д. Значение примитивной переменной определяется некоторым подмножеством возможных значений данной категории. В итоге тип описывает полный набор грамматических значений слова. Пример записи полностью определенного типа: a1(b11, d1), где [a1]=имя сущ., [b1]=им. падеж, [c1]=ед. число, [d1]=муж. род.

Типизированные объекты V – языка: константы Сiaj(…), переменные Xiaj(…) , операционные константы Viaj(…) (aj(…) – условная запись типа, приписанного объекту) используются для конструирования V – формул, которые и описывают синтаксические связи между словами предложения. Синтаксис записи формул описывается следующим образом:

1. <V - формула>::=<терм>

2. <терм>::=<простой терм>|<составной терм>

3. ><составной терм>::=<опер. константа>(<список термов>)

4. <список термов>::=<терм>|<терм>,<список термов>

5. <простой терм>::=<об. константа>|<об. переменная>

6.<об. константа>::=C<ID><тип>

7.<об. переменная>::=X<ID><тип>

8.<опер .константа>::=V<ID><тип>

Константа соответствует начальной форме слова анализируемого предложения, ее тип описывает реальные грамматические значения слова. Переменная в отличие от константы соответствует некоторому множеству подразумеваемых в контексте предложения слов. Операционные константы соответствуют принятым в естественном языке правилам согласования  слов в таких синтаксических конструкциях, как словосочетания, обороты и предложения. Пример полностью определенной формулы для предложения «густой туман быстро рассеялся»: V5(V2(C1,C2),V9(C3,C4)). Такая формула не содержит переменных,в таком качестве она описывает конкретное предложение текста. Частично определенная формула содержит переменные и описывает некоторое семейство предложений, так формула V5(V2(C1,C2),V9(C3,X)) соответствует семейству предложений «густой туман быстро X», где X может быть любым глаголом, согласуемым с существительным “туман” в числе и роде.

3.3. Модель предметной области

Модель предметной области (МПО) определяется словарями семантического обеспечения СПТ. Назначение МПО – определить “смысл” слов анализируемых предложений, сформировав тем самым понятия. Таким образом, машинное понимание заключается в том, чтобы оценить слова анализируемых предложений в терминах заложенной МПО, и тем самым, придать им некоторый смысл. Основными компонентами МПО являются: модели семантических характеристик (СХ) и семантических отношений.

СХ используются для смыслового разделения лексического материала предметной области [8]. Следует различать непосредственно семантические характеристики и их значения, во втором случае используется сокращение ЗСХ. Наличие семантической характеристики указывает точку смыслового дробления лексики, тогда как ее значения определяют непосредственно области, получаемые в результате такого дробления. Модель СХ определяется как двухосновная алгебраическая система без операций с двумя отношениями , где D – множество семантических характеристик, B – множество значений семантических характеристик, R1 – отношение на D x B, R2 – отношение на B x D. Cвойства отношений R1и R2 позволяют дать модели следующую графическую интерпретацию  (рис. 7).

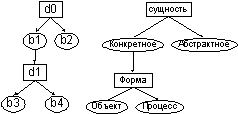
Рис.7. Графическая интерпретация модели СХ.

Значения СХ (овалы на рис. 7) объединяются в наборы, которые затем приписываются словам анализируемых предложений в процессе семантического анализа, в результате чего формируются «осмысленные» понятия. Важной чертой модели M1 является отношение семантической совместимости ЗСХ, вытекающее из заложенных в модель свойств.

Это отношение позволяет для любой пары ЗСХ отметить наличие элементарной смысловой совместимости или ее отсутствие. Совместимые значения не противоречат друг другу на рис. 7 это {b1,b3}, {b1,b4}. Несовместимые значения имеют противоречивый смысл, например: {b1,b2}, {b3,b4}, {b3,b2}. Наборы ЗСХ объединяют только совместимые значения. В качестве иллюстрации предположим, что слову «туман» был приписан набор ЗСХ «конкретное, объект» в одном контексте и ЗСХ «конкретное, процесс»  - в другом. Оба набора не могут быть объединены, так как одна и та же «сущность» не может одновременно сочетать в себе свойства «объекта» и «процесса». СПТ сделает вывод о наличии двух разных понятий, поскольку слова имеют несовместимый противоречащий друг другу смысл. Следует отметить, что приведенные рассуждения относятся к модели на рис. 7, тогда как для некоторой другой модели одновременная сочетаемость свойств «объекта» и «процесса» может быть вполне нормальной.

Поскольку семантический анализатор оперирует не со словами и предложениями, а с V – формулами и их элементами (см. рис. 6), формируемые понятия имеют следующий вид , где - константа V – языка, выделенная во входной формуле, совместимых ЗСХ модели M1. Такое представление соответствует гипотезе «о репрезентации понятий признаками» (см. [2]). Понятия являются промежуточным результатом работы СПТ. В выходных структурах межфразового семантического анализатора (рис. 6), участвуют не понятия, а концепты, которые имеют следующий вид  , где - переменная V – языка, t - набор семантически совместимых ЗСХ модели M1. Такое представление соответствует гипотезе «о множественной репрезентации понятий» (см. [2]).

Кроме M1 предметная область описывается вторым компонентом – моделью семантических отношений, которая используется механизмом семантического анализа для извлечения и формирования понятий из входных V – формул.

Модель семантических отношений определяется как четырех основная алгебраическая система вида . Где L – множество семантических отношений, определенных в предметной области, N – конечное подмножество натуральных чисел, T – множество наборов семантически сочетаемых ЗСХ, F – множество частично определенных формул V – языка. R4 – отношение на декартовом произведении L x N,  R5 – отношение на декартовом произведении R4 x T, R6 – отношение на декартовом произведении L x F. Отношения R4, R5 и R6 имеют следующую интерпретацию. Каждая пара (l,n) R4 определяет n-ого возможного участника отношения l, где n используется для уникальной идентификации участников внутри отношения l. Каждая пара ((l,n),t) R5 определяет  набор ЗСХ, характерный для n-ого участника отношения l. При этом сам участник не определен, известны только характерные для него ЗСХ, заключенные в наборе t. Каждая пара (l,f) R6 определяет характерную для отношения l синтаксическую конструкцию ЕЯ, описываемую частично определенной V – формулой f. Каждой переменной формулы f соответствует некоторый n-ый участник отношения l. Таким образом, имея на входе семантического анализатора полностью определенную V – формулу fi, и подобрав подходящую пару (l,f) R6 модели M2 можно, путем сопоставления fi и f выделить константы из входной формулы и, приписав этим константам наборы ЗСХ соответствующих участников отношения l, сформировать понятия вида .

В качестве примера работы семантического анализатора рассмотрим отношение ДЛИТЕЛЬНОСТЬ некоторой модели M2. Данное отношение может быть описано следующим образом: ДЛИТЕЛЬНОСТЬ L – семантическое отношение, (ДЛИТЕЛЬНОСТЬ,1) R4,(ДЛИТЕЛЬНОСТЬ,2)R4– идентификация первого и второго участников ((ДЛИТЕЛЬНОСТЬ,1),{конкретное, процесс}) R5 – набор ЗСХ первого участника, ((ДЛИТЕЛЬНОСТЬ,2),{абстрактное}) R5– набор ЗСХ второго участника, (ДЛИТЕЛЬНОСТЬ,V5(X1;V4(C;X2))) R6 – формула V – языка, описывающая синтаксическую конструкцию, принятую в ЕЯ для отражения данного отношения, где значение константы C есть глагол «длиться». Приведенная формула описывает семейство предложений вида «X1 длится X2». Если СПТ выделит в тексте предложение: «заседание длилось один час». То по результатам сопоставления  V – формулы V5(C1;V4(C2;V3(C3,C4))), соответствующей данному предложению, с шаблоном V5(X1;V4(C1;X2)), будет выявлено, что X1=C1 и X2=V3(C3,C4). Это в свою очередь на основе приведенных данных об отношении ДЛИТЕЛЬНОСТЬ позволит выделить понятие o1=(C,{конкретное, процесс}) и o2=(V3(C3,C4),{абстрактное}), это означает, что слово «заседание» воспринято СПТ, как некоторый процесс, а словосочетание «один час» - как некоторая абстрактная сущность.

3.4. Семантическое представление текста

Семантическое представление текста формируется из семантических представлений отдельных предложений [7], элементами которых являются понятия, извлеченные из анализируемого текста, и выявленные между ними семантические отношения модели M2. Семантическое представление отдельных предложений описывается алгебраической системой, подобной графу, у которого вершинами являются понятия, а любое ребро помечено семантическим отношениям и соединяет те вершины-понятия, которые находятся друг с другом в данном отношении.  Идентификаторы участников записываются в виде меток при каждой вершине. Такая структура именуется в данной работе семантической сетью (см. [10]) отдельных предложений, формируемых на выходе семантического анализатора (рис. 6). На рис. 8 приведена графическая интерпретация двух семантических сетей для предложений: «Туман сгустился над центром озера. У берегов он наоборот рассеялся»

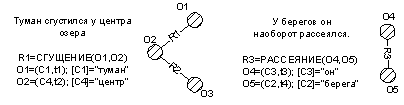
Рис. 8. Семантический образ предложений.

Конечная смысловая структура текста представляется четырех основной алгебраической системой вида (6), называемой семантической сетью естественного текста. Где Ot – множество концептов выделенных в тексте, At – множество ребер, связывающих концепты из Ot,Lt L – множество семантических отношений, выявленных в тексте, и используемых в качестве меток ребер из At. Ht – множество классов, связывающих концепты из Ot по классовой семантической совместимости их наборов ЗСХ, которая отличается от обычной семантической совместимости, рассмотренной ранее, тем что элементарная совместимость требуется не для всех пар ЗСХ сопоставляемых концептов, а только для некоторой, оговоренной группы, характерной для целого класса концептов. R1t – отношение инцидентности на Ot x At x N, где N – подмножество идентификаторов участников отношений модели M2. R2t – отношение инцидентности на At x Lt, RH – отношение классовой принадлежности на Ot x Ht. Такая довольно громоздкая структура получается после нестрогого отождествления понятий из семантических образов отдельных предложений, в процессе которого образуются концепты. Рис. 9 иллюстрирует процесс «склеивания» семантических сетей предложений, представленных на рис. 8, в единую сеть.

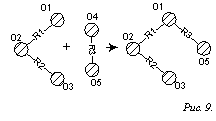
Рис. 9. Процесс «склеивания» семантических сетей предложений.

В данном примере отождествлению подлежат понятие O1, соответствующее существительному «туман», и понятие O4,соответствующее местоимению «он».

Особенностью результирующей сети на рис. 9 является то, что O1 становится не понятием, а концептом, поскольку после нестрогого отождествления оно имеет структуру , где - переменная, множество возможных значений которой образуется словами {«туман», «он»}, t - результирующий набор ЗСХ, полученный при объединении наборов ЗСХ отождествленных понятий O1 и O4.

3.5. Классификация на основе синтаксиса

Идея использовать более сложную модель текста при решении задач текстовой обработки, по сравнению с моделью терм-документ и полиграммной моделью, не нова. В [4] наряду с частотной информацией предложено учитывать результаты синтаксического анализа в числовых весах слов обрабатываемых текстов. Согласно этому предложению, вес слова есть функция от частоты его встречаемости, набора грамматических значений и синтаксической роли в предложении. Так при равной частоте встречаемости больший вес получают имена существительные в роли подлежащего, затем – в роли прямого и косвенного дополнения и т.д.

Эта идея может быть существенно расширена за счет использования V – языка. В нем отсутствуют традиционные понятия подлежащего, дополнения и т.п., тем не менее, существует более строгий способ указания синтаксической роли слов, который основан на  операционных константах языка. Функция модификации частотного веса слова имеет вид , где V – множество операционных констант языка,N1 – подмножество натуральных чисел, D – множество весовых коэффициентов. Значение функции d = (Vi,nj) следует трактовать следующим образом: роль nj – ого аргумента Vi – ой операционной константы оценивается весом d. Функция задается таблично при определении V – языка. В качестве примера рассмотрим следующий вариант функции (таб. 1). Согласно таб. 1 для формулы V2(C1,C2) объектная константа C2 получит вес 2, а объектная константа C1 – вес 1. Рассмотрим гипотетический пример фрагмента утвердительного предложения: «плотный туман рассеивался быстро».  Здесь выделяются следующие константы C1, C2,C3, C4. (типы констант не указаны). Согласно принятым в V – языке обозначениям семантические значения этих констант следующие: [C1]=«плотный», [C2]=«туман», [C3]=«рассеивался», [C4]=«быстро»

Табл 1. Фрагмент табличного задания функции .

В соответствии с правилами согласования (таб. 1), данному предложению ставится в соответствие формула F1=V5(V2(C1,C2),V9(C3,C4)). Далее, используя функцию , для слов[C1], [C2], [C3], [C4] получаются следующие весовые коэффициенты: W[C1]=(V2,1)=1,W[C2]=(V2,2)=2, W[C3]=(V9,1)=2, W[C4]=(V9,2)=1, для словосочетаний [V2(C1,C2)] и [V9(C3,C4)] - W[V2(C1,C2)] = (V5,1) = 5, W[V9(C3,C4)] = (V5,2) = 5. Окончательные веса для слов могут быть получены простым суммированием их собственных весов с весами тех конструкций, в которых они встречаются. Для данного примера W[C1]=1+5=6, W[C2]=2+5=7, W[C3]=2+5=7, W[C4]=1+5=6

Приведенный способ весовой оценки может быть использован как дополнение к весам, полученным частотным методом. Далее модифицированные веса могут применяться в любом алгоритме классификации документов, основанных на взвешивании терминов.

Другой способ применения V – языка в задаче классификации может быть отражен при описании самих классов. Идея такого подхода заключается в представлении описаний классов F в (1) в виде наборов V – формул, возможно частично определенных. Частично определенная формула кроме объектных типизированных констант Ci содержит так же переменные Xj. Примером частично определенной формулы может послужить следующая модификация приведенной ранее: F2=V5(V2(C1,C2),X). F2 описывает множество предложений вида: «плотный туман ‘выполняет действие X’».  Наборы подобных формул закладываются в описаниях классов, а сам алгоритм классификации заключается в выполнении сопоставлений вида F1=F2, где F1 – формула предложения анализируемого документа, F2 – частично определенная формула в описании класса.

3.6. Классификация на основе семантики

Классификация на основе семантического представления развивает идею, предложенную в предыдущем подразделе. При решении задачи классификации описание каждого из классов представлено в виде модели Mc, отвечающей (6). Документы, поступающие на вход классификатора, подвергаются обработке модулями СПТ (рис. 5-6). В результате такой обработки на выходе СПТ для каждого текстового документа получается семантическое представление Mi, так же отвечающее (6). Задача классификатора заключается в сопоставлении семантических представлений Mc и Mi, результатом которого является вывод о принадлежности данного документа классу. Как видно, ключевым моментом в такой постановке задачи является определение правила, по которому выполняется сопоставление Mc и Mi.Данное правило может использовать все или только некоторые компоненты представления (6). Рассмотрим некоторые частные случаи.

1. Используется только Lt. Документ относится к классу, если выполнено условие LcLi, т.е. в тексте выявлены все отношения, присущие классу.

2. Используется только Ot. Документ относится к классу, если выполнено условие OcOi, т.е. в тексте выявлены все понятия, присущие классу.

3. Используется Ot и Ht. Документ относится к классу, если . В соответствии с этим требованием, все понятия, выявленные в тексте документа и вошедшие в один класс эквивалентности H' представления Mc, так же должны входить в один класс эквивалентности H’’семантического представления документа Mi.

4. Используется R1t и R2t. Документ относится к классу, если выполнено условие , т.н. в тексте выявлены все понятия и отношения между ними, присущие классу.

Кроме указанных случаев возможна разработка специфических правил, а так же их совместное комбинирование. 

Заключение

Рассмотренные в данной статье методы классификации ТЕЯ обладают следующими характерными особенностями.

Нейросетевые классификаторы просты в реализации в случае применения моделей терм-документ и полиграммной модели представления текста, удобны в обучении, поскольку для этого требуется минимальное участие эксперта, а так же позволяют выбирать оптимальное с точки зрения пользователя соотношение точность/полнота за счет настройки числовых пороговых параметров в алгоритмах обучения. С другой стороны, низкая адекватность указанных моделей представления текста приводит к принципиальному барьеру, которым фиксируется отношение точность/полнота, за счет чего обе характеристики не могут быть более улучшены. Такое положение дел приводит к необходимости разрабатывать более сложные модели текста, такие как семантическая сеть, предложенная в данной работе.

Следует так же отметить, что способы построения классификаторов не ограничиваются изложенными в данной статье. В настоящее время существует множество работающих систем (в том числе и в сети Интернет), построенных по традиционным принципам, коротко затронутым в данной статье, но детальный анализ которых выходит за рамки ее темы. Авторы убеждены, что рассмотренный здесь нейросетевой подход и разработанный метод семантического анализа являются перспективными направлениями в области решения задач интеллектуальной обработки текста, в том числе и автоматической классификации. 

Литература

1. Alberto Muñoz Compound Key Word Generation from Document Databases Using A Hierarchical Clustering ART Model, 1997

2.Гаврилова Т.А., Червинская К.Р. Извлечение и структурирование знаний для экспертных систем. – М.: Радио и связь, 1992.

3. Дж Солтон. Динамические библиотечно-поисковые системы. М.: - Мир, 1979.

4. Ермаков А.Е., Плешко В.В. Синтаксический разбор в системах статистического анализа текста. // Информационные технологии. – 2002. – N7.

5. Круглов В.В., Борисов В.В. Искусственные нейронные сети.Теория и практика. – М.: Горячая линия – Телеком, 2001.

6. Леонтьева Н.Н. К теории автоматического понимания естественных текстов. Ч.2: Семантические словари: состав, структура, методика создания – М.: Изд-во МГУ, 2001

7. Леонтьева Н.Н. К теории автоматического понимания естественных текстов. Ч.3: Семантический компонент. Локальный семантический анализ. – М.: Изд-во МГУ, 2002

8. Рубашкин В.Ш. Представление и анализ смысла в интеллектуальных информационных системах. – М.: Наука, 1989.

9. Тейз А., Грибомон П., Юлен Г. и др. Логический подход к искусственному интеллекту. От модальной логики к логике баз данных: Пер.с франц.  – М.: Мир, 1998.

10. Уэно Х., Кояма Т., Окамото Т. и др. Представление и использование знаний: Пер. с япон. – М.: Мир, 1989.

11.  Ф. Уссермен Нейрокомпьютерная техника. - М.: Мир, 1992.

12.   Андреев А.М.,Березкин Д.В.,Сюзев В.В., Шабанов В.И. Модели и методы автоматической классификации текстовых документов// Вестн. МГТУ. Сер. Приборостроение. М.:Изд-во МГТУ.- 2003.- №3.

13.   Искусственный интеллект. - В 3-х кн. Кн.2.Модели и методы: Справочник. /Под ред. Д.А. Поспелова. – М.: Наука, 1990.