Стандарты аутентификации и ЭЦП России и США

А. Винокуров

Исторически первой и в течение длительного времени единственной задачей криптографии как прикладной дисциплины была защита от несанкционированного ознакомления с содержимым корреспонденции и личных записей. Этот факт отражен и в самом названии дисциплины: криптография переводится с греческого как «тайное письмо» Приоритет данной задачи прослеживается и в новейшие времена: первый в мире стандарт шифрования данных был принят в США более четверти века назад и долгое время оставался единственным стандартизованным криптографическим алгоритмом. В СССР аналогичный стандарт был разработан примерно в те же сроки, хотя рассекречен был значительно позже.

Новые задачи криптографии

В эпоху бумажной переписки задачи из области защиты корреспонденции, такие, как обеспечение подлинности текстов и подтверждение их авторства, решались естественным образом, на основе характеристик физических носителей информации. Подлинность и авторство определялись по почерку и собственноручной подписи.

Ситуация начала меняться только с появлением цифровых систем передачи, хранения и обработки данных. А с возникновением и широким распространением глобальных сетей ЭВМ проблема обеспечения целостности цифровой информации перешла в разряд критических: старые подходы оказались совершенно непригодными для ее решения. Шифрование данных обеспечивает секретность, но в общем случае не может защитить их от случайных или преднамеренных искажений. Поэтому для выявления фактов искажений информации необходимо принимать дополнительные меры. В настоящее время существует две постановки задачи защиты целостности и подтверждения авторства цифровых данных.

Первая и более простая относится к информационному обмену в условиях взаимного доверия сторон. В этом случае необходимо обеспечить механизм, позволяющий получателю убедиться в том, что данные пришли именно от отправителя и не были искажены «по дороге». Во второй помимо первого требования есть и другое: у получателя не должно быть возможности изготовить подложные данные от имени отправителя. Такая постановка задачи предполагает отсутствие доверия между сторонами.

Подходы и методы решения обоих видов задачи существенно различаются. Все возрастающая актуальность проблемы привела к тому, что ведущие государства мира уже приняли соответствующие криптографические стандарты. В настоящей статье делается попытка сравнительного анализа подходов к ее решению, закрепленных в системе стандартов России и США.

Стандарты имитозащиты данных

Системы криптографических стандартов России и США предусматривают алгоритмы имитозащиты - защиты от навязывания противником ложных данных. Эта же методика позволяет подтвердить авторство информации в условиях взаимного доверия между отправителем и получателем, но не защищает ее от подделки со стороны получателя. Именно поэтому ее иногда называют «симметричной цифровой подписью », что, конечно, терминологически небезупречно.

В обоих стандартах защита строится по одному и тому же принципу: вырабатывается отрезок данных, называемый имитовставкой, или кодом аутентификации данных (data authentication code, DAC), который передается или хранится вместе с защищаемыми данными. Имитовставка зависит от секретного ключа и всего массива данных весьма сложным образом, поэтому подделать ее, не зная ключа, невозможно. Так как секретный ключ известен только двум (или некоторой группе) корреспондентов, то получение сообщения, защищенного имитовставкой, выработанной на данном ключе, подтверждает принадлежность автора сообщения к этой группе.

Алгоритм выработки имитовставки

В российской системе стандартов описание алгоритма выработки имитовставки содержится в тексте ГОСТ 28147-89 [2] и названо режимом выработки имитовставки. В американской системе за это отвечает отдельный документ - FIPS 113 [3], в котором приведено описание алгоритма аутентификации данных (data authentication algorithm, DAA).

Алгоритм выработки имитовставки в обоих стандартах строится на базе алгоритма зашифрования в режиме гаммирования с обратной связью. Именно в этом режиме шифрования последний блок гаммы зависит от всех предшествующих блоков открытого текста. Имитовставка является отрезком данных размера l бит, где l не превышает размера блока, при ее выработке используется зашифрование блоков в режиме простой замены:

При необходимости последний неполный блок данных (T_N) дополняется до размера полного блока нулевыми битами.

Таким образом, как уже было отмечено выше, процедура выработки имитовставки очень похожа на зашифрование данных в режиме СВС или СРВ (гаммирования с обратной связью). Имитовставка выбирается из старшей части блока, полученного после последнего преобразования. Вероятность навязывания ложных данных противником равна 2^-l.

Существуют различия в выработке имитовставки в стандартах России и США: в американском стандарте используется полный цикл простой замены Е_K, а в российском - укороченный цикл, в котором реализованы первые 16 раундов преобразования. Упрощенный цикл выработки имитовставки в российском стандарте позволяет выполнять ее примерно вдвое быстрее шифрования, в американском же -скорости обеих процедур одинаковы.

В отечественном стандарте биты имитовставки извлекаются из той половины блока, которая модифицируется на последнем раунде преобразования. Поскольку последний раунд цикла выработки имитовставки отличается от последнего раунда циклов шифрования тем, что в нем выполняется перестановка старшей и младшей частей блока, а на раунде модифицируется старшая его часть, то биты имитовставки следует выбирать из младшей половины — этим обусловлено различие в вышеприведенных выражениях для I.

И как следствие, в российском стандарте размер имитовставки не превышает половины размера блока, т.е. 32 бит, а в американском - полного размера блока, т.е. 128 бит. Иногда это может оказаться немаловажным фактом.

Если с помощью имитовставки необходимо контролировать также возможность изъятия или повторной передачи всего реально переданного сообщения целиком, то при выработке имитовставки может использоваться служебная информация, например номер переданного сообщения и/или дата и время передачи. Таким образом, имитовставка, или код аутентификации данных, в российском и американском стандартах шифрования вырабатываются сходным образом, алгоритмы их получения различаются в отдельных не очень существенных деталях.

Стандарты электронно-цифровой подписи

Бурное развитие информационных технологий приводит к тому, что в сфере защиты информации постоянно возникают новые задачи. Одной из таких задач является подтверждение авторства сообщений, что абсолютно необходимо для дистанционного управления ресурсами.

Эволюция ЭЦП

Действительно, лицо, управляющее чьими-либо ресурсами по распоряжениям владельца, должно обладать возможностью доказать, что выполненное им распоряжение было получено именно от владельца. Данная задача стала особенно актуальной с появлением электронной коммерции, в качестве ресурса здесь выступают деньги на банковском счету владельца. Для ее решения были предложены различные схемы электронно-цифровой подписи (ЭЦП). Первая схема ЭЦП - RSA - была разработана еще в конце 1970-х годов. Однако проблема подтверждения авторства стала актуальной настолько, что потребовалось установление стандарта, только в 1990-х годах, во время взрывного роста глобальной сети Интернет и массового распространения электронной торговли и оказания услуг. Именно по указанной причине стандарты ЭЦП в России и США были приняты практически одновременно, в 1994 году [4,5].

Из предложенных криптологами схем ЭЦП наиболее удачными оказались RSA и схема Эль-Гамаля. Но первая из них была запатентована в США и ряде других стран (патент на RSA прекратил свое действие совсем недавно). Во второй же схеме существует большое количество ее возможных модификаций, и все их запатентовать весьма затруднительно. Именно по этой причине схема ЭЦП Эль-Гамаля осталась по большей части свободной от патентов. Кроме того, эта схема имеет и определенные практические преимущества: размер блоков, которыми оперируют алгоритмы, и соответственно размер ЭЦП в ней оказались значительно меньше, чем в RSA, при той же самой стойкости. Именно поэтому стандарты ЭЦП России и США базируются на схеме Эль-Гамаля [6].

Принцип построения ЭЦП

В схемах симметричной (одноключевой) криптографии, в частности в алгоритмах шифрования и выработки имитовставки, оба участника информационного обмена разделяют один и тот же секретный ключ, который можно вырабатывать как простой массив из случайных или псевдослучайных битов. Асимметрия ролей отправителя и получателя в схемах ЭЦП требует наличия двух тесно связанных ключей: секретного, или ключа подписи, и открытого, или ключа проверки подписи. Строго говоря, второй из них ключом не является, так как ключ по определению обязан быть секретным, так что «открытый ключ» -нечто вроде «сухой воды». Но термин прижился в литературе, и мы будем его придерживаться.

Любая схема ЭЦП обязана определить три следующих алгоритма:

алгоритм генерации ключевой пары для подписи и ее проверки;

алгоритм подписи;

алгоритм проверки подписи.

В табл.1 приведены уравнения преобразования данных для каждого из этих алгоритмов в стандартах ЭЦП России и США.

Как видно из табл. 1, стандарты России и США очень похожи, они различаются лишь некоторыми числовыми параметрами и отдельными деталями выработки ключевой пары, вычисления и проверки подписи. Действительно, оба стандарта являются вариантами одной и той же схемы ЭЦП Эль-Гамаля.

Новые стандарты ЭЦП

Последние достижения теории вычислительной сложности показали, что общая проблема логарифмирования в дискретных полях, являющаяся базой указанной схемы ЭЦП, не может считаться достаточно прочным фундаментом. Например, размеры блоков, считающиеся «безопасными», растут сравнительно быстрыми темпами. В результате это привело к тому, что стандарты ЭЦП России и США в 2001 году были обновлены: переведены на эллиптические кривые [7, 8]. Схемы ЭЦП при этом остались прежними, но в качестве чисел, которыми они оперируют, теперь используются не элементы конечного поля GF(2n) или GF(p), а эллиптические числа - решения уравнения эллиптических кривых над указанными конечными полями. Роль операции возведения числа в степень в конечном поле в обновленных стандартах выполняет операция взятия кратной точки эллиптической кривой - «умножение» точки на целое число.

Надлежащий выбор типа эллиптической кривой позволяет многократно усложнить задачу взлома схемы ЭЦП и уменьшить рабочий размер блоков данных. Старый российский стандарт ЭЦП оперирует 1024-битовыми блоками, а новый, основанный на эллиптических кривых, - 256-битовыми, и при этом обладает большей стойкостью.

Стойкость схемы подписи ГОСТ Р34.10-94 базируется на сложности решения задачи дискретного логарифмирования в простом поле. В настоящее время наиболее быстрым алгоритмом ее решения для общего случая является алгоритм обобщенного решета числового поля.

В ГОСТ Р34.10-2001 стойкость схемы ЭЦП основана на сложности решения задачи дискретного логарифмирования в группе точек эллиптической кривой. При правильном выборе параметров кривой самыми эффективными методами ее решения являются более трудоемкие r- и l-методы Полларда. Так, по разным оценкам специалистов [6], трудоемкость взлома старого и нового стандартов ЭЦП России составляет величину порядка 1026 и 1038 операций умножения в базовом поле GF(p) соответственно. Очевидно, что новый стандарт более стойкий.

Стандарты на хэш-функции

Блоки данных, которые могут быть подписаны непосредственно, ограничены по размеру: они не могут выходить за пределы используемой при работе алгоритмов разрядной сетки. В то же время может возникнуть потребность разработки ЭЦП для документа произвольного размера. Чтобы преодолеть данное ограничение, в схемах ЭЦП принято подписывать не непосредственно электронный документ, а результат его преобразования к блоку данных фиксированного размера, называемого хэшем (hash) сообщения.

Алгоритм выработки хэша должен обладать следующими свойствами:

постоянством размера - для входного массива данных произвольного размера результатом должен быть блок данных фиксированного размера;

вычислительной необратимостью -для заданного хэша не должно быть способа подбора массива данных под него более эффективным способом, чем перебор по возможным значениям массива данных;

свободой от коллизий - не должно существовать вычислительно эффективного способа поиска двух массивов данных с одинаковым значением хэша.

Алгоритмы хэширования

Алгоритмы хэширования, или хэш-функции, помимо использования в схемах ЭЦП могут применяться и самостоятельно в схемах защиты информации. Например, с их помощью можно вырабатывать ключ шифрования из пароля. В системах криптографических стандартов России и США содержатся определения алгоритмов хэширования. В России он устанавливается стандартом ГОСТ Р34.11-94 [9], а в США - документами FIPS 180-1 и FIPS 180-2 [10|. Отечественный стандарт хэширования был принят в 1994 году и с тех пор не изменялся, размер хэш-блока для него составляет 256 бит.

В США изначально действовал стандарт SHS (secure hash standard), где размер хэш-блока был равен 160 бит. Однако в 2002 году стандарт был пересмотрен: прежний остался действовать и получил обозначение SHA-1, но к нему были добавлены три новых алгоритма, вырабатывающие хэш-блоки размером 256,384 и 512 бит, названные SHA-256/384/512 соответственно.

В российском и американском стандартах используются принципиально различные подходы к построению хэш-функции. В стандарте РФ для его выработки применяется процедура шифрования по стандарту ГОСТ 28147-89, в стандарте США этот алгоритм полностью самостоятельный. Как следствие, стандарт РФ определяет не один, а целое семейство хэшей, поскольку параметром используемого шифра является набор узлов замены. Для каждого набора получаем собственный хэш. Это может быть преимуществом, но может и порождать проблемы совместимости. С внешней точки зрения оба хэша построены по одинаковому принципу: каждый из них определяет шаговую функцию хэширования, которая принимает на входе 2 блока данных: «текущее» значение хэша с предыдущего шага и очередной фрагмент входного массива данных. Внутреннее же устройство шаговых функций совершенно различное: в американском стандарте SHA-1 эта функция устроена по итерационному принципу и состоит из 80 достаточно несложных раундов, остальные хэш-функции построены аналогично. В российском стандарте хэширования шаговая функция хэширования состоит из линейных перемешиваюих операций и четырех зашифрований по ГОСТ 28147-89 в режиме простой замены, служащих основным источником сложности и нелинейности хэширующего преобразования. Для сравнения шаговые функции обоих стандартов приведены в табл. 2.

Соответствующие схемы преобразования данных при хэшировании по ГОСТ Р34.11-94 и SHA-1 показаны на рис. 1 и 2 соответственно. Из приведенных данных ясно, что сложность американского стандарта хэширования ниже, чем у российского. Российский стандарт предполагает выполнение четырех зашифрований за один цикл выработки хэша, или в общей сложности 128 раундов. Каждый раунд шифрования требует примерно полтора десятка элементарных машинных операций, что существенно увеличивает затраты машинного времени на выполнение линейных перемешивающих операций. Один раунд выработки хэша SHA-1 гораздо проще: он весь может быть реализован примерно за 15-20 команд, общее количество раундов всего 80, и за один цикл выработки хэша «обрабатывается» вдвое больше исходных данных - 512 против 256 в ГОСТ P34.ll. Таким образом, можно предположить, что быстродействие программных реализаций SHA-1 будет примерно в 3-6 раз быстрее, чем у отечественного стандарта.

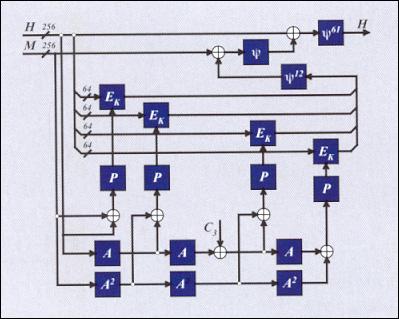
Рис. 1. Схема преобразования данных при хэшировании по ГОСТ Р34.11-94:

А, ψ - линейные перемешивающие преобразования;
Р - перестановка байтов;
E_K - операция зашифрования по ГОСТ 28147-89;
С₃ = const

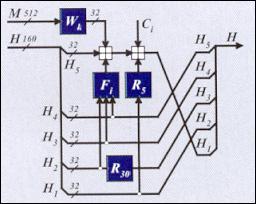
Рис. 2. Схема преобразования данных при хэшировании по SHA-1:
F_i - нелинейные функции, 1 ≤ i ≤ 4,
W_k - функции выработки 32-битовых элементов из 512-битового блока данных;
C_i - константы, где 1 ≤ i ≤ 4,
R_i - операция циклического сдвига аргумента на i бит влево

Помимо обычной функции хэширования, система американских стандартов определяет функцию выработки хэша, зависящего от ключа [11]. Аналог данного алгоритма в системе российских стандартов отсутствует. Однако это не является проблемой, так как достаточно легко внести изменения в обычную процедуру хэширования, сделав результат зависящим от секретного ключа. Для этого достаточно добавлять секретный ключ к массиву хэшируемых данных, так что необходимость в отдельном стандарте хэша, зависящего от ключа, не очевидна.

Выводы

В настоящее время системы криптографических стандартов имитозащиты данных и электронно-цифровой подписи России и США весьма схожи по номенклатуре и характеру алгоритмов. Стандартные алгоритмы выработки имитовставки построены практически по одному и тому же принципу и базируются на национальных стандартах шифрования. Что касается стандартов ЭЦП, то здесь наблюдается практически полное соответствие: стандарты ЭЦП России и США базируются на родственных модификациях схемы ЭЦП Эль-Гамаля и отличаются рядом несущественных деталей. Совсем недавно эти стандарты были обновлены - переведены на «эллиптические кривые». Подобная поспешность может свидетельствовать в пользу того, что государственные структуры продвинулись в изучении проблемы дискретного логарифмирования в конечных полях несколько дальше, чем сообщество, ведущее открытые исследования в криптографии. Кроме того, практическая синхронность принятия и обновления стандартов ЭЦП в России и США может говорить в пользу того, что оба государства находятся на примерно одном и том же уровне в научных исследованиях в области криптографии.

Из всей системы стандартов наиболее сильно различаются стандарты хэширования. Российский стандарт определяет единственный алгоритм с размером блока 256 бит, тогда как американский стандарт задает целое семейство хэш-функций с разными размерами хэш-блока. Кроме того, система стандартов США определяет алгоритм хэширования с результатом, зависящим от секретного ключа, тогда как в российской системе стандартов ничего подобного нет. Однако следует отметить, что в отечественной системе стандартов подобный алгоритм и не нужен, так как он может быть легко построен на основе обычного алгоритма хэширования.